How Beams are Sized

Checking a uniformly loaded simple beam in bending:

Determining Beam Load

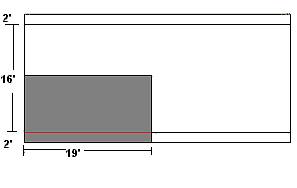
This is a rectangular wood beam supported on both ends and loaded evenly along its length. A rafter, joist, girder or header is often a beam of this type. We need to know what the load is on the beam. Use as an example a door header with a 19' clearspan on a 16 foot wide building that has 2 foot overhangs.

The combined Live Load and Dead Load on the building's roof is 50 pounds per square foot. The area in gray shows the portion of the roof bearing on the beam, 19' X 10'...190 square feet. Multiply that by 50 pounds of weight on every square foot = 9500 pounds bearing on the beam.

Fiberstress in Bending: What The Calculator Does

In order to find the section modulus required we need to find the maximum bending moment and divide it by the allowable fiberstress for the species and grade you enter into the calculator. The formula for finding the maximum bending moment is:

	Mmax = WL/8
	Working the Example:
	Mmax = (9500 X 19) / 8
	Mmax = 22562.5 Ft/Lbs

To find the section modulus required we need to divide the maximum bending moment in inch pounds by the allowable fiberstress:

	Section Required = Mmax X 12 / Fb
	Sreq = (22562.5 X 12) / 1150 lbs/sq in
	Sreq = 270,744 in/lbs / 1150 PSI
	Sreq = 235.4 inches³

We are looking for a beam with a section modulus of 235.4 in³ The formula for determining section modulus for a rectangular beam is:

	S = bd² / 6
	Let's try a 6 X 8
	S = 6 X (8 X 8) / 6
	S = 6 X 64 / 6
	S = 64 in³

We needed a value of 235.4 or greater, we have 64...not even close. Try again with an 8X14 it comes to 261.3...that works as does a 10 X 12 at 240 in³
The calculator does the moment and section modulus required calculations after you enter the load, span, size, and Fb values. There is a link to a table of NDS values for many grades and species on the calculator page

Joist Sizing:

A joist is basically a small beam, normally considered to be uniformly loaded. Around here they are typically designed for a 40 or 50 pounds per square foot loading. A joist is normally limited by deflection, it gets too bouncy or sags enough to crack plaster before it is in fiberstress trouble, always work all the checks to be sure though.

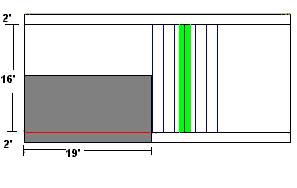
Going back to our same example, lets run 16' floor joists across the right side of the building on 16" centers. Each joist will support an area halfway to each adjoining joist. 8" along one side and 8" along the other side, 16" wide by 16' long. The joists are in blue, the area of bearing on one is in green.
(192" X 16") / 144 = 21.33 square feet
21.33 SF X 50 PSF = 1066 pounds

I like yellow pine for joists, I'm guessing it will take a pretty decent 2X12 so will start with a no.2. Don't forget to plug in actual dimensions, in this case I'll plug in 1.5 x 11.25. Run it and it comes up larger than needed in fiberstress and fine on deflection (I used loblolly)...try to economize go to a 2 x 10, deflection fails, too bouncy. As a rafter with the same loading the 2 x 10 would be fine, more deflection is allowed there, Fb typically limits rafters. Shear is fine. I have this in tables...that would be the correct way to spec this, My CABO book says that 2 x 12 is good out to 19' 1" and a 2 x 10 is only good to 15' 8". CWC book says 18'10" and 16'1" respectively. Now with wall framing the span will work by code at 2 x 10, its near the limit, judgement call, I would bump up if at all possible. Code is limiting to 1/360 span deflection (a 15' span would deflect 1/2" at design load). Many floors are now specced at 1/480, consumers are wanting stiffer floors nowadays. Rafter? Same way, just use horizontal clearspan not the angled run length, deflection can be up to 1/180 span. These are minimums, you can always go bigger.

Deflection: What the Calculator Does

The formula for deflection is:

	D =(5 * W * L³) / (384 * E * (b * d³/ 12))
	Working the Example:
	D =(5 * 1066 * 192"³) / (384 * 1600000E * (1.5b * 11.25d³/ 12))
	D = .345" Design deflection

You Have entered a 1066 lb load, 192" span, Modulus of Elasticity of 1.6 million, 1.5" width and 11.25" depth.
The calculator also checks what the maximum allowable deflection for the span entered is,

	D = L/360
	D = 192"/ 360
	D = .533" Allowable deflection

The deflection of .345" is less than the allowable deflection of .533 so the 2x12's work in deflection.

Shear: What The Calculator Does

	Shear =(( 3 / 2 )* V ) / ( bf * df )
	Shear =(( 3 / 2 )* 533 ) / ( 1.5 * 11.25 )
	Shear = 47.37 PSI

The Calculator halves the load of 1066 lbs to give V a value of 533 lbs. Yellow pine has an allowable horizontal shear of 90 PSI, the 47.37 PSI design shear passes.

The calculator checks for the section needed and the section provided,

	Section Required =(v (bf df))/ Fv
	Section Required =(47.37 (1.5 11.25))/ 90
	Section Required =8.88"²

We input a section of 16.875 sq" so are fine in shear.

Back to Beam Calculator